[4강] Introduction to Neural Networks
오늘 강의 내용은 backpropagation과 neural network 이다.
<복습>
classifer를 어떻게 정의하는지는 함수 f를 통해 알 수 있다. x가 입력값이고 weights W를 파라미터로 가지로 있고 출력값(output)은 분류하고자 하는 클래스에 대한 score vector이다. 또한, loss function도 배웠는데 loss function은 데이터 항의 조합으로 이루어져 있는데 정규화 항을 포함하고 있다. 정규화 항은 얼마나 우리의 모델이 단순한지 더 나은
일반화를 위해 적합한 단순 모델을 가지고 있는지를 표현하게 해준다. 또한, 우리는 최적의 loss를 갖게 하는 파라미터 W를 찾고자 했다. 그래서 loss function의 W에 관한 gradient를 찾았다. 최적화를 통해 gradient가 음수인 방향, 즉 경사가 하강하는 방향을 반복적으로 구해 아래로 나아갈 수 있고, 결국에는 가장 낮은 loss를 찾을 수 있다. gradient를 구하는 다른 방법은 수학적으로 유한 차분 근사(finite differnce approximation)를 이용해 계산할 수 있다.
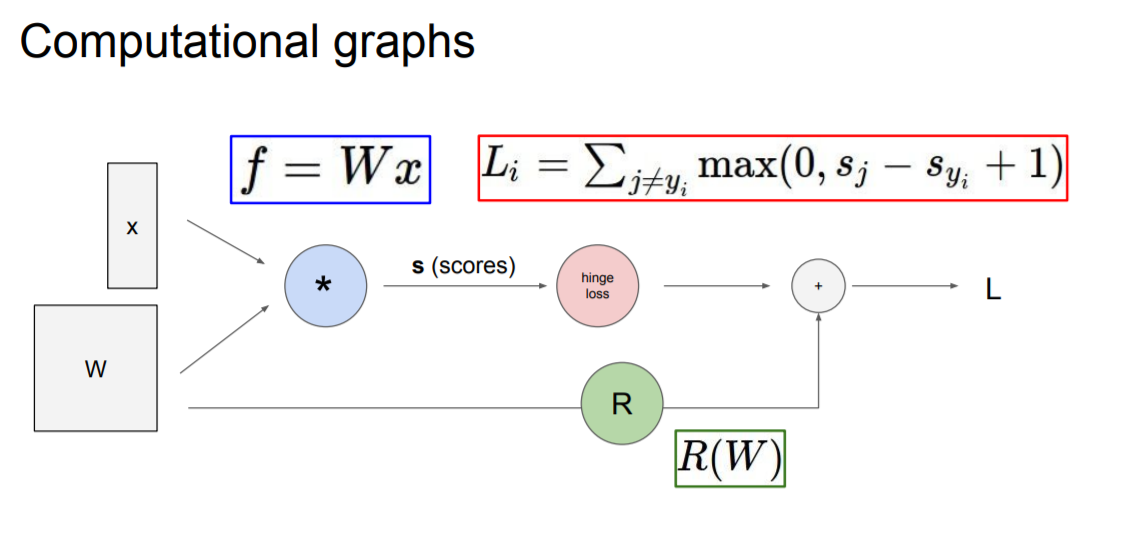
computational graph는 그래프를 이용해서 어떤 함수든지 표현할 수 있게 해준다. 그래프의 각 노드는 연산 단계를 나타낸다. 밑에 예제는 input이 x, W인 선형 classifier이다. hinge loss라는 계산노드를 통해 데이터 항 Lᵢ를 계산한다. 노드 R은 regularization 항을 우리의 최종 loss는 L은 regularization 항과 데이터 항의 합이다. computational graph를 사용해서 함수를 표현하게 됨으로써 우리는 backpropagation이라고 부르는 기술을 사용할 수 있게 되었다.
<backpropagation>
Backpropagation은 gradient를 얻기위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용한다. backpropagation은 우리가 매우 복잡한 함수를 이용하여 작업할때 아주 유용하게 사용된다 (예를 들면 CNN).
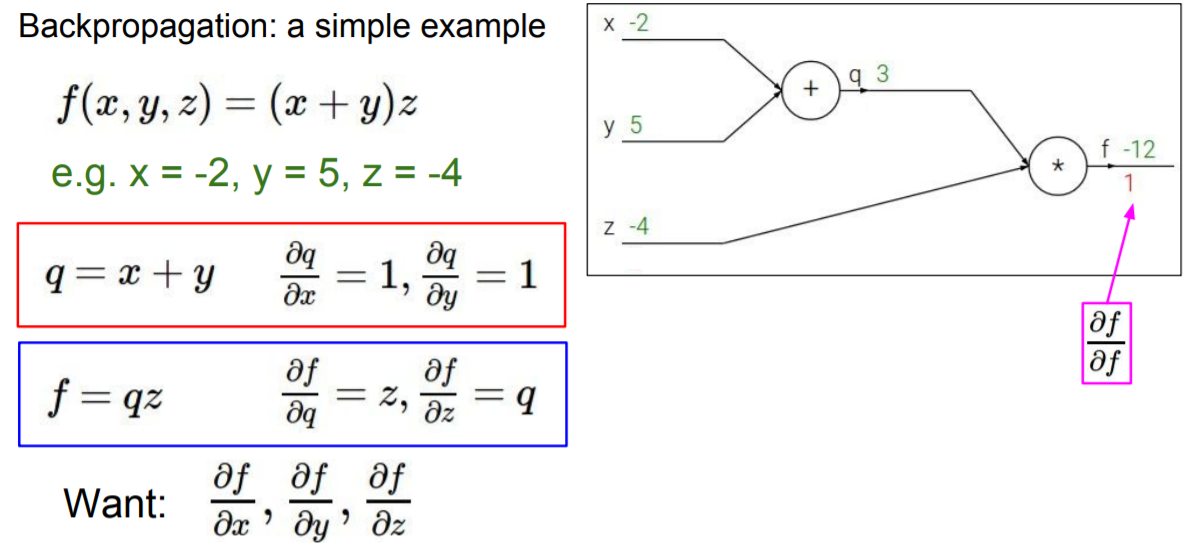
밑에 예제는 backpropagation의 간단한 예제이다. 이 경우 x,y,z로 구성된 function f는 (x+y)*z와 같다. 그리고 우리는 f의 출력에 대한 어떤 변수의 gradient를 찾기 원한다. 첫번째 단계는 항상 함수 f를 computational graph로 나타내는 것이다. x는 -2, y는 5, z는 -4이고 최종 노드를 통과하면 -12를 얻는다. 이 때 모든 중간 변수에 이름을 줄 것이다. x+y 덧셈 노드를 q라고 부르고 f는 q*z가 된다. q와 z에 대한 f의 gradient는 곱셈규칙에 의해 각각 z와 q이다. backpropagation은 chain rule의 재귀적인 응용으로 chiain rule에 의해 뒤에서부터 시작한다.
1. 출력의 f에 대한 gradient를 계산하면 1이다.
2. z에 대한 f의 미분은 q이다. 그리고 q의 값은 3이다. 그래서 z에 대한 f의 미분값은 3이다.
3. q에 대한 f의 미분값은 z와 같고 여기에서 z는 -4이다. 그래서 q에 대한 f의 미분값은 -4이다.
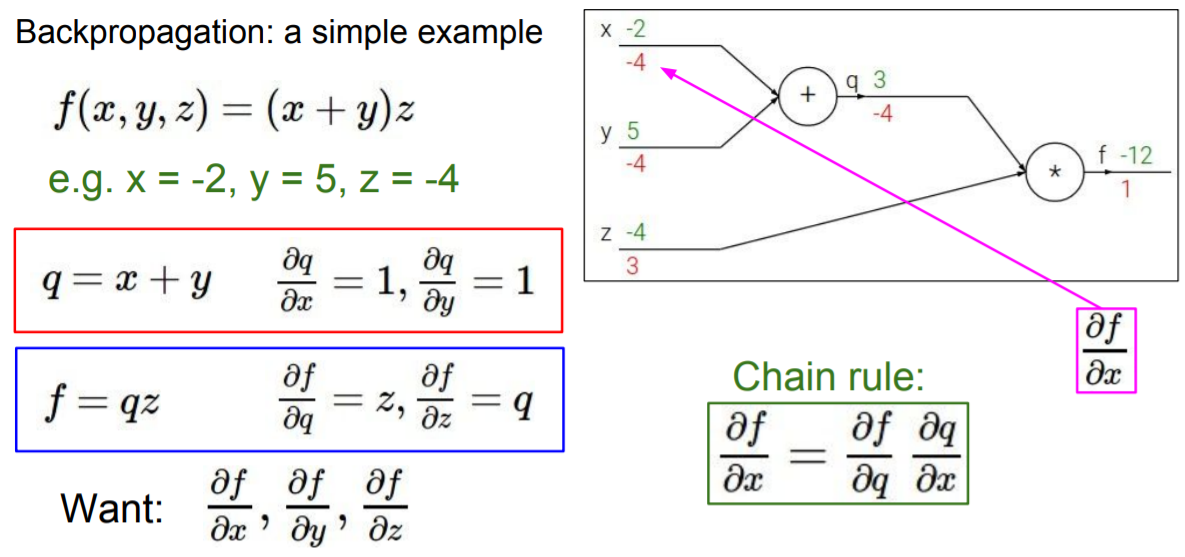
4. y에 대한 f의 미분값은 어떻게 구할까? y와 f는 바로 연결되어있지 않지만 f는 z와 연결되어있다. 이 때 우리는 chain rule을 이용해 y에 대한 f의 미분은 q에 대한 f의 미분과 y에 대한 q의 미분의 곱으로 나타낼 수 있다. 그래서 -4이다.
5. 마지막으로 f에 대한 x의 gradient는 -4 * 1 이므로 -4이다.
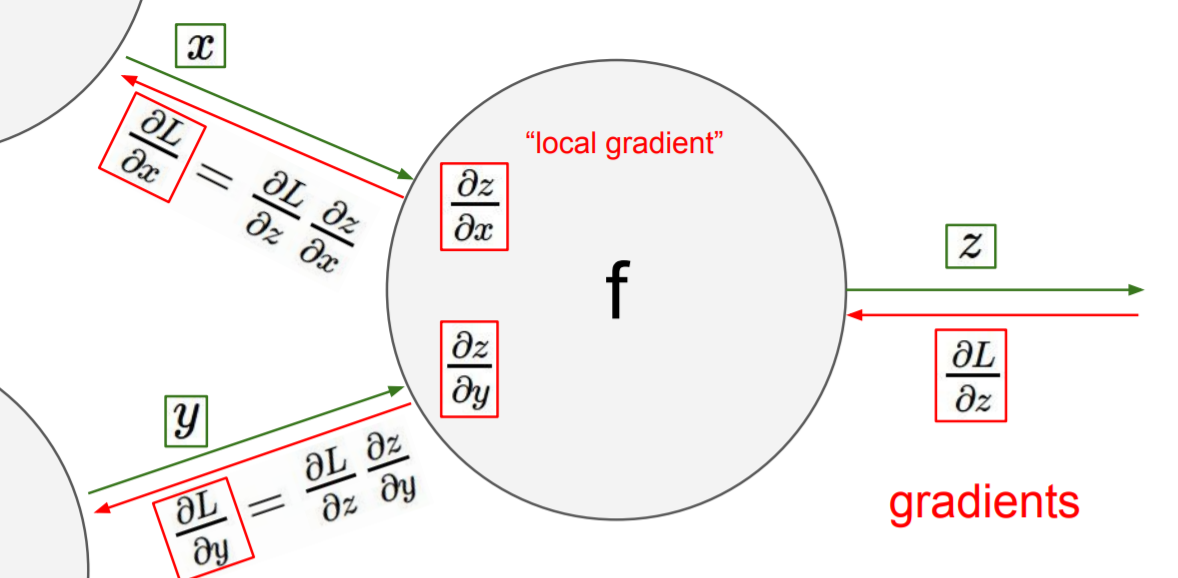
local gradient를 구할 수도 있다 (들어오는 입력에 대한 출력의 기울기: z에서 x에 대한 gradient를 구할 수 있으며 y에 대한 gradient). 각 노드는 local 입력을 받고 밑에 보이는 것처럼 다음 노드로 출력값을 보낸다.
Backpropagation의 다른 예제를 보자. 여기에서 최종 변수에 대한 출력의 gradient는 1이다. 이제 뒤로 한 스텝 간다. 1/x 이전의 input에 대한 gradient는 얼마일까? upstream gradient는 1이다. 우리가 가지고 있는 f는 1/x 이고, 이것의 local gradient인 x에 대한 f의 미분은 -1/x^2와 같다 (빨간 박스 참고). 그래서 우리는 -1/x^2를 x에 대입한다. (x)은 1.37이고,이 변수에 대한 우리의 최종 gradient는 1/-1.37^2 * 1 = -0.53이다.
다음 노드로 넘어가면 upstream gradient는 -0.53이다. 그리고 현재 노드는 +1이다. (x+상수)에 대한 local gradient는 1이다. chain rule를 사용하면 upstream gradient는 -0.53이고, 우리의 local gradient는 1이기 때문에 gradient 는 -0.53 이다.
한 단계 더 진행해보면 upstream gradient는 -0.53이고 local gradient는 exponential 노드에서, chain rule에 의해 gradient가 -0.53*e^x임을 알 수 있다. (x의) 값이 -1인 경우 (exponential 노드에서) 최종 gradient는 -0.2이다.
다음 노드는 -1과 곱하는 노드이다. upstream gradient는 -0.2이고 local gradient는 local gradient는 x에 대한 f의 미분임으로 -1이다 (1 * -1). 그렇기 때문에 gradient는 -1 * -0.2 = 0.2이다.
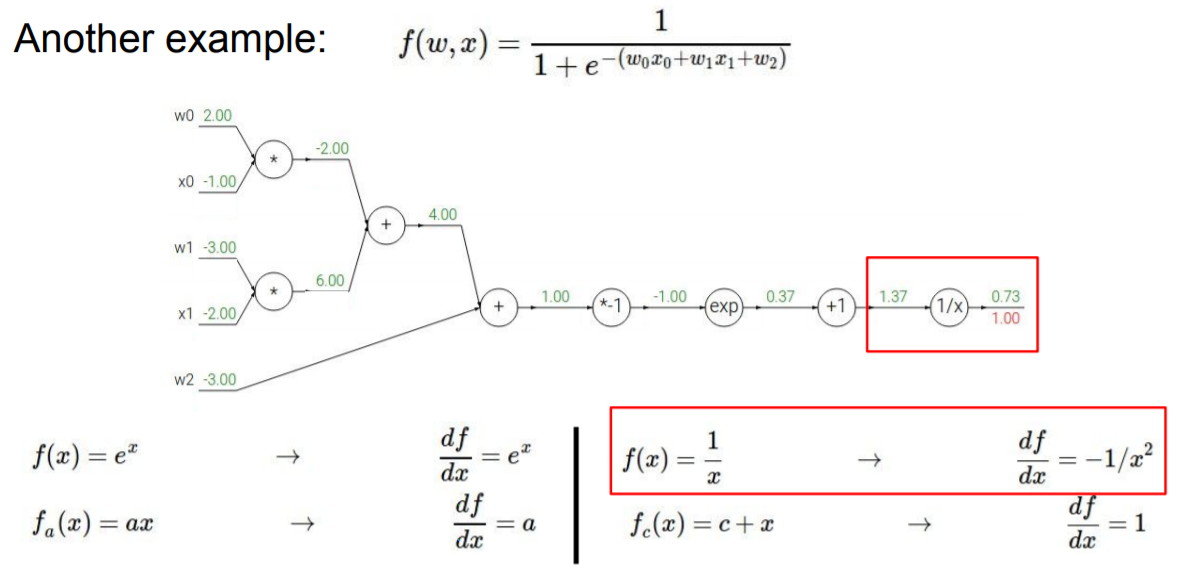
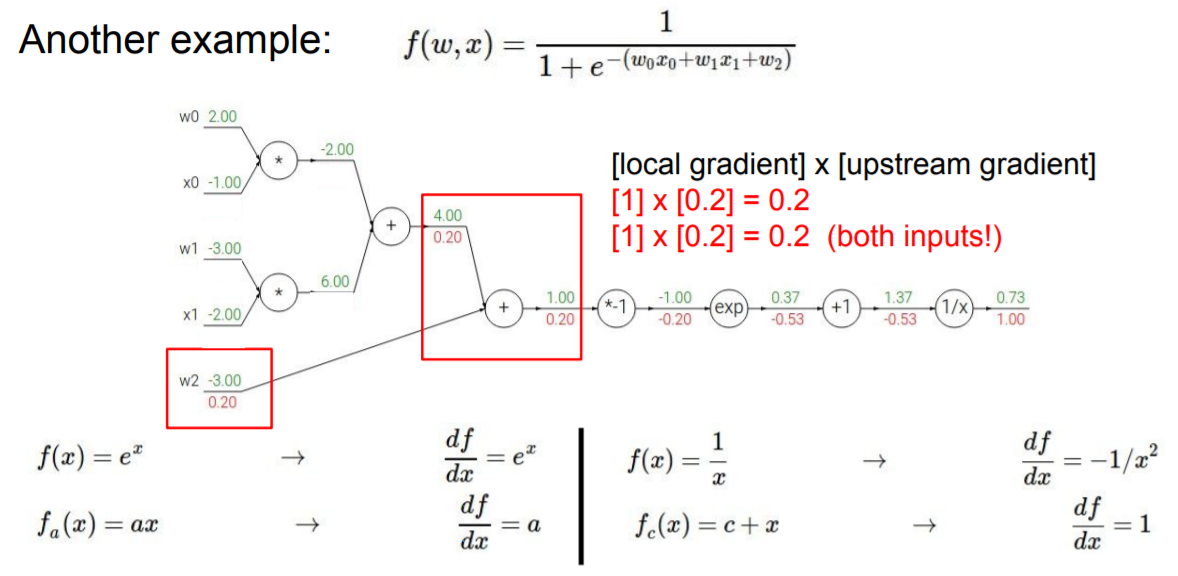
덧셈노드에서 두개의 노드와 연결된다. upstream gradient는 0.2이다. 이전의 간단한 예제에서 덧셈 노드를 가지고 있을 때 덧셈 노드에서, 각 입력에 대한 local gradient는 1이었다. 여기에서 local gradient는 upstream gradient 0.2와
한번 곱해질 것임으로 1 * 0.2 = 0.2이다. 이것은 아래 브랜치에서도 똑같이 적용되 총 gradient는 0.2 이다.
w₀과 x₀이 있는곳까지 가면 여기에서는 곱셈 노드를 가지고 있다. 이전에 보았던 곱셈 노드에서 input에 대한 gradient는
한 인풋에 대하여 다른 인풋의 값이었다. 이 경우 w₀에 대한 gradient는 -0.2이다. 아래에 있는 다른 하나(x0)는 -1이기 때문에 -1과 0.2를 곱해 -0.2를 얻게된다. x0에 대해서도 같은 과정을 반복하면 0.2 * 2를 하게 되므로 0.4를 얻는다.
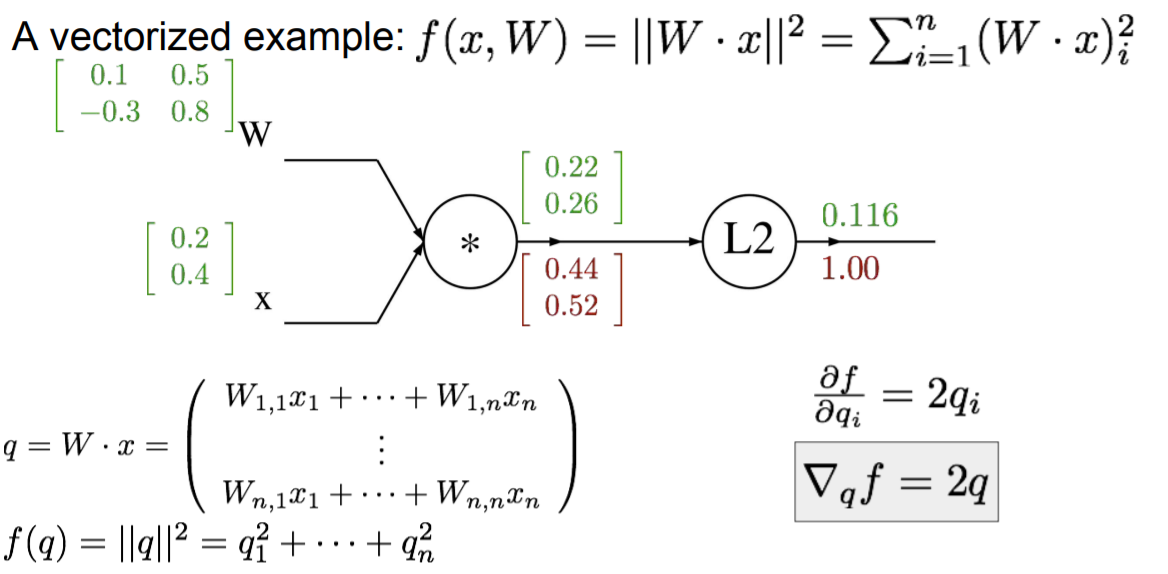
이제 computational graph보다 구체적인 벡터화 된 예제를 보자. x와 W에 대한 함수 f는 x에 의해 곱해진 W의 L2와 같다. 그리고 이 경우 x를 n-차원이라고 하고, W는 n*n이라고 한다. 최종출력에 대한 gradient는 1이다. 이것은 항상 첫 단계이다.
한 노드 뒤로 이동하면 L2 이전의 중간 변수인 q에 대한 gradient를 찾아야된다. q는 2차원의 벡터이다. 우리가 찾고 싶은 것은 의 각각의 요소가 f의 최종 값에 어떤 영향을 미치는지이다. 밑에 식을 보면 도함수를 구했을 때 벡터의 형태로 쓰면 벡터 q에 대해서 2를 곱한 것이라는 것을 알 수 있다. 그래서 각 요소를 2로 곱한 gradient 0.44와 0.52를 얻었다.
W의 gradient는 무엇일까? 여기서 다시 chain rule를 사용해야된다.

<Summary>
Backpropagation는 신경망의 핵심 기술이고, gradient를 구하기 위해서 backpropagation을 썼다. Backpropagation는 computational graph에서 chain rule을 재귀적으로 적용한 것이다. forward pass에서 우리는 연산 결과를 계산하고 결과를 저장한다. 이것은 나중에 우리가 gradient를 계산할 때 backward pass에서 chain rule을 사용하기 위한 것이고 upstream gradient와 저장한 값들을 곱해 각 노드의 input에 대한 gradient를 구하고 그것들을 연결된 이전 노드로 통과시킨다.

<Neural Networks>
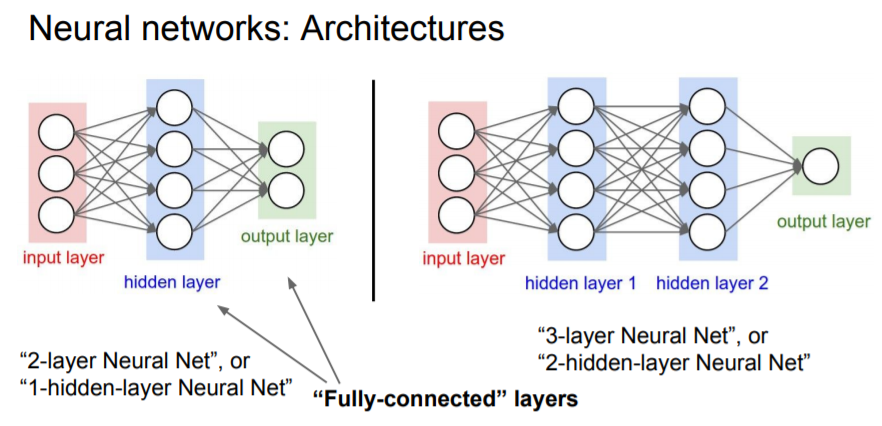
위에 식은 선형 변환식이고 다른 하나는 2층짜리 신경망의 레이어이다. 위에는 W1과 x의 행렬 곱이고 우리는 이것의 중간값을 얻고 max(0, W)라는 비선형 함수를 이용해 선형 레이어 출력의 max를 얻는다. 선형 레이어들을 쌓는다면 그것들은 결국 선형 함수가 되기 때문에 비선형 변환은 매우 중요하다. 밑에 예제를 보면 우리는 첫번째 선형 레이어를 가지고 있고 그 다음 비선형 레이러를 가지고 있다 그리고 그 위에 선형 레이어를 추가함으로 최종적으로 score 함수를 얻을 수 있다. 신경망은 함수들의 집합(class)이다. 비선형의 복잡한 함수를 만들기 위해서 간단한 함수들을 계층적으로 여러개 쌓아올린 것이다 (계층적 계산).

'AI > CS231n' 카테고리의 다른 글
| [6강] Training Neural Networks I (0) | 2020.11.14 |
|---|---|
| [5강] Convolutional Neural Networks (0) | 2020.11.07 |
| [3강] Loss Functions and Optimization (0) | 2020.10.30 |
| [2강] Image Classification (0) | 2020.10.17 |
| [0강] 딥러닝 기초 이론 스터디 - CS231n (0) | 2020.10.10 |
댓글
이 글 공유하기
다른 글
-
[6강] Training Neural Networks I
[6강] Training Neural Networks I
2020.11.14 -
[5강] Convolutional Neural Networks
[5강] Convolutional Neural Networks
2020.11.07 -
[3강] Loss Functions and Optimization
[3강] Loss Functions and Optimization
2020.10.30 -
[2강] Image Classification
[2강] Image Classification
2020.10.17